Do you have a similar problem that would require STATA help? We have the best econometrics homework help tutors to assist you. Just click the button below:
We need to regress log wheat yield on location, temperature, precipitation, and cultivar dummy variable on stata. Specifically, we consider the following multiple regression model with fixed effects to estimate the weather effect on wheat quantity:
yijt =γi + τj + α1t + α2t2 + f(Xjtβ) + Eijt ———————————— (1)
where yijt denotes the log wheat yield for variety i at trial location j in year t; γi is a vector of cultivar intercepts to control; τj denotes a vector of location intercepts to control; α1t + α2t2 captures the time trend, and f(·) represents the weather function while Xjt is a vector of weather related variables and the β are the slope parameters for Xjt; Eijt is the error term.
Precisely, we add intercepts γi to control for genetic differences in yield and τj to control for spatially-invariant unobserved effects such as soil quality. The time trend is included in this model as a quadratic form to capture the genetic improvements at a diminishing rate over time . Since only elite lines are likely tested and developed in the trial area, this property needs to be reflected. Next, we cluster standard errors by year, which takes account of random correlation among unobservables within the same period.
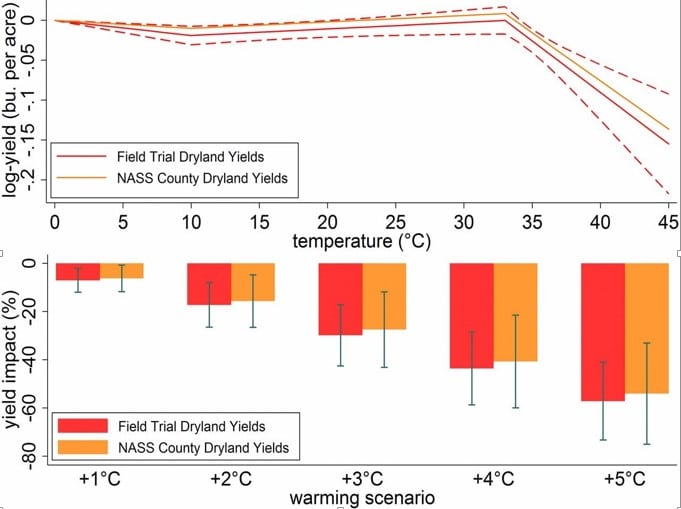
We presumes the nonlinear relationship between temperature and quantity rather than linearity. In other words, we assume that when the climate is below or above a certain threshold, two dependent variables – quantity and quality – may decline dramatically. From this point of view, we use the function for capturing weather effects as follows:
f(Xjt;β) = β1lowjt + β2medjt + β3highjt + β4Pjt + β5Pjt2 ——————– (2)
where β1lowjt measures degree days from 0 to the lower threshold, 10 Celsius degree, β2medjt measures degree days between 11 and the upper threshold, 26 Celsius degree, and β3highjt measures degree days above the upper threshold, 27 Celsius degree, β4Pjt and β5Pjt2 indicates a quadratic effect of precipitation during the growing season on wheat yield.
Do you need econometrics assignment help on a similar question. Click the button below and we will be glad to help you.